Numerical cognition
Numerical cognition is essential to many aspects of life and arithmetic abilities predict academic achievements better than reading. In recent years, researchers strive to understand the building blocks of numerical cognition, the neural tissue involved, and the developmental trajectories. An example for atypical development is developmental dyscalculia (DD) which is a congenital deficiency in the development of arithmetic abilities.
We are interested in basic mental operations involved in numerical cognition. For example, we study processes involved in the association of symbols (e.g., digits, words) with quantities, and brain structures that underlie these processes. The picture that appears here (a small 8 trying to climb the ladder to the top of a big 3) represents the fact that digit symbols have their own physical features (e.g., physical size) that may modulate their symbolic (i.e., numerical value) effect. These physical sizes could be employed to ask questions about digit representation and usage. For example, in our culture 8 represents a larger value or size than 3, hence, the appearance of 8 as (physically) smaller than 3 might produce a conflict. Namely, 8 has a larger numerical value than 3 but in this picture it is physically smaller than 3. Psychologists have been using similar conflict situations to study automaticity and selective attention.
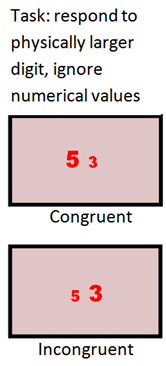We use the comparative judgment task in which a participant is presented with two numbers (e.g., 3 5) and asked to decide which one is numerically larger/smaller. This task gives rise to the distance effect-people respond faster when the two digits are further apart from one another (e.g., 3 8) than when they are close to one another (e.g., 6 8). It is possible to create a Stroop-like situation in which the digits differ not only in numerical value but also in physical size (e.g., 3 5). Commonly, people respond faster to congruent (e.g., digits that are both numerically and physically smaller/larger) than to incongruent pairs of digits-the size congruity effect. This suggests that people process the numerical values automatically (even when they are irrelevant to the task). In contrast, those with developmental dyscalculia show deficiencies in automatic processing of numerical values. Moreover, the size congruity effect involves the intraparietal sulcus (IPS) and deficiency presented by people with developmental dyscalculia might involve this area.
For more information: https://en.wikipedia.org/wiki/Numerical_Stroop_effect
In collaboration with the laboratory of Dr. Ronen Segev, from the department of life sciences, we started to study the Archer fish (see research in pictures and archer fish). Here we aim to study how animals without a developed cortex can execute various tasks such as comparative judgment or Stroop-like.
In collaboration with Professors Joseph Tzelgov and Andrea Berger from BGU and Dr. Orly Rubinsten from University of Haifa, we received from the Israel Science Foundation (ISF) support for a center of excellence to study the neurocognitive basis of numerical cognition. In addition, we recently received an ERC Advanced Researcher Grant to study effects of non-countable dimensions, i.e., the perception and evaluation of sizes and amounts, on numerical cognition. The grant title is: Size matters in numerical cognition.
Selected publications
Ashkenazi, S., Henik, A., Ifergane, G., & Shelef, I. (2008).Basic numerical processing in left intraparietal sulcus (IPS) acalculia.Cortex, 44, 439-448.
Rubinsten, O., & Henik, A. (2009). Developmental dyscalculia: Heterogeneity may not mean different mechanisms. Trends in Cognitive Sciences, 13, 92-99.
Ashkenazi, S., & Henik, A. (2010).A disassociation between physical and mental number bisection in developmental dyscalculia.Neuropsychologia, 48, 2861-2868.
Naparstek, S., & Henik, A. (2010). Count me in! On the automaticity of numerosity processing.Journal of Experimental Psychology: Learning, Memory, and Cognition, 36, 1053-1059.
Henik, A., Leibovich, T., Naparstek, S., Diesendruck, L., & Rubinsten, O. (2012).Quantities, amounts, and the numerical core system.Frontiers in Human Neuroscience,5:186. doi: 10.3389/fnhum.2011.00186
Naparstek, S., & Henik, A. (2012). Laterality briefed: Laterality modulates performance in a numerosity-congruity task. Consciousness and Cognition, 21, 444-450.
